Desto weiter man in die Tiefen der Mathematik absteigt umso schwieriger werden die Fragestellungen. Eines dieser Probleme ist das Gradientenverfahren bzw. Gradientenabstiegsverfahren oder auch das Verfahren des steilen Abstiegs. Doch eigentlich ist es gar nicht so schwer, sobald man es nur einmal verstanden haben. Gucken wir es uns mal an…
Was ist das Gradientenverfahren? Eine kurze Definition…
Das Gradientenverfahren ist eine Methodik aus der numerischen Mathematik zum lösen von Optimierungsproblemen. Mit dem Verfahren wird das Minimum oder Maximum einer Funktion ermittelt. Sucht man das Minimum einer Funktion können synonym die Begriffe Gradientenabstiegsverfahren oder Verfahren des steilsten Abstiegs verwendet werden.
Es gilt hierbei jedoch zu beachten, dass das gefundene Minimum bzw. Maximum je nach Startpunkt unterschiedlich sein kann. Das ist dadurch zu erklären das eine Funktion mehrere Maxima bzw. Minima haben kann und das Verfahren abbricht wenn keine weitere Verbesserung in der Suchrichtung gefunden werden kann. Wir bleiben also in einem lokalen Minimum bzw. Maximum hängen und finden den globalen Extrempunkt nicht.

Wie geht der Abstieg?
Die Grundlegende Idee des Gradientenabstiegsverfahrens besteht darin das man mit Hilfe des Gradienten einer Funktion eine Suchgerade bildet. Auf dieser Suchgeraden kann man man dann Schritt für Schritt näher auf das Minimum zugehen. Dabei machen wir es uns zunutze das ein Gradient immer in die Richtung des höchsten Anstiegs einer Funktion zeigt.
Das heißt, dass der entgegengesetzte Gradient auch in die Richtung des höchsten Abstiegs zeigt.
Um also das Gradientenabstiegsverfahren anzuwenden benötigst du:
- eine Funktion deren Minimum du suchst
- einen Startpunkt
Gradientenabstiegsverfahren Schritt für Schritt
Wenn du diese beiden Sachen hast können wir auch schon loslegen. Ich erkläre dir hier die Grundlegenden Schritte des Gradientenabstiegsverfahrens mit Hilfe einer Beispielfunktion.
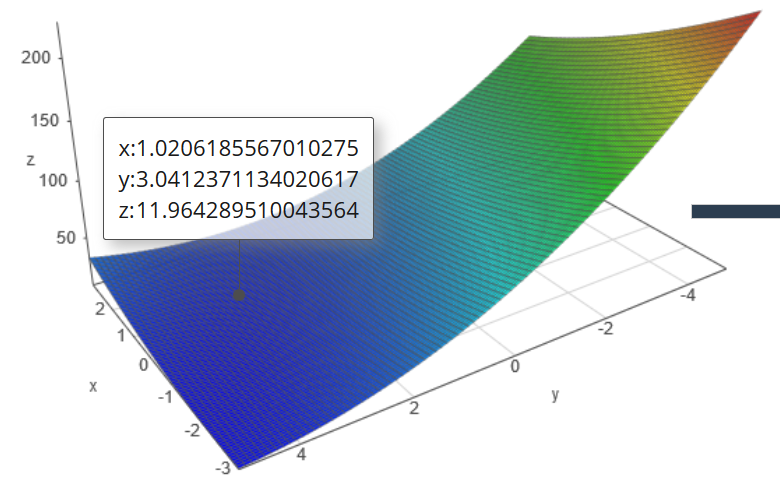
Beispiel Funktion: \( f(x)=x^2+2y^2+2xy-6x-16y+41 \) mit dem Startpunkt \( P=(1, 3)\)
- Bilde den Gradienten deiner Funktion
Bei dem Gradientenabstiegsverfahren dreht sich alles um den Gradienten, also musst du zu aller erst den Gradienten deiner Funktion bilden.
Der Gradient ist ein Vektor der aus den partiellen Ableitungen der Komponenten einer Funktion besteht. Unsere Funktion hat zwei Komponenten: x und y.
Das heißt der Gradient unserer Funktion ist ein Vektor mit Zwei Komponenten.
Um die partielle Ableitung einer Komponente zu bilden betrachten wir alle Glieder der Formel in der diese Komponente vorkommt und leiten die ab.
Die partiellen Ableitungen sind also: \(f_x(x,y)= 2x + 2y – 6 \) und \(f_y(x, y) = 2x + 4y -16\).
Damit sieht unser Gradient wie folgt aus:
\( \nabla f(x,y) = \left (\begin{array} 22x+2y-6 \\ 2x + 4y -16\end{array}\right)\) - Einsetzen des Startpunktes in den Gradienten
Nun bestimmen wir den Gradienten ausgehend von unserem Startpunkt \(P=(1,3)\). Also einfach den Punkt einsetzten.
\( \nabla f(1,3) = \left (\begin{array} 22 \cdot 1 + 2 \cdot 3 – 6 \\ 2 \cdot 1 + 4 \cdot 3 -16 \end {array}\right) =\left( \begin{array} 22 \\ -2 \end{array} \right) \)
- Normieren des Gradienten
Bei einem normierten Gradienten beträgt die Länge exakt 1, da das in den meisten fällen nicht zutrifft müssen wir den Gradienten zu aller erst normieren bevor wir ihn für unsere Suchgerade verwenden können. Um einen Vektor auf die Länge 1 zu normieren wird er mittels Skalarmultiplikation mit seiner derzeitigen Länge dividiert. Logisch, wenn du eine Zahl durch sich selbst teilst kommst du immer auf 1 ;D
Die Länge des Gradienten ermittelst du indem du den Betrag bildest, also:
\( | \nabla f(1,3) | = \sqrt{2^2 + (-2)^2} = \sqrt 8 \approx 2,83\)
Nachdem du die Länge ermittelt hast heißt es nurnoch jede Komponente durch die Länge zu teilen:
\( || \nabla f(1,3)|| = \left(\begin{array} 22 \\ -2 \end{array} \right ) \cdot \frac {1}{2,83} = \left(\begin{array} 00,707 \\ -0,707 \end{array} \right) \) - Aufstellen der Suchgeraden
In diesem Verfahren bewegen wir uns entlang einer Geraden und versuchen auf dieser Geraden den kleinsten Punkt zu finden. Dank des Gradienten wissen wir ja das uns diese Gerade in die Richtung des größten Abstiegs führt und damit auch irgendwann zum Minimum. Die Suchgerade nenne ich hier \( v(x)\).
Zum Aufstellen einer Geraden benötigen wir einen Richtungsvektor – also unseren Gradienten, einen Startpunkt – das ist immer der aktuell kleinste gefunde Punkt und einen Parameter, ich nenne den hier \( \lambda\), aber du kannst ihn natürlich nennen wie du willst ;D . Der Parameter bestimmt wie groß die Schritte sind die wir auf unserer Suchgeraden machen. Du definierst dein Parameter direkt zu Beginn. Ich gebe ihm hier den Wert 1.
Grundsätzlich hat eine Gerade die Form:
\( v(x) = Ortsvektor + \lambda \cdot Richtungsvektor \)
Gut, unsere Geradengleichung sollte also wie folgt aussehen:
\( v(x) =\left(\begin{array} 11\\ 3 \end{array} \right) + 1 \cdot -\left(\begin{array} 00,707\\-0,707 \end{array} \right ) \)
Wenn wir das nun ausrechnen erhalten wir:
\( v(x) = \left(\begin{array} 00,29 \\ 3,71 \end{array} \right)\)
als neuen Punkt.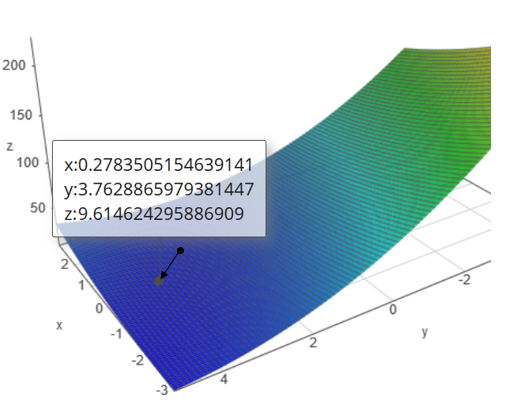
- Nun müssen wir noch überprüfen ob sich der Funktionswert verbessert hat
Um zu ermitteln ob sich der Funktionswert verbessert hat müssen wir lediglich die beiden Punkte, also den Startpunkt und den neuen ermittelten Punkt in die Funktionsgleichung einsetzen und gucken was rauskommt, also:
\( f(1,3) = 1^2 + 2 \cdot 3^2 + 2 \cdot 1 \cdot 3 – 6 \cdot 1 -16 \cdot 3 = 12 \)
\( f(0,29; 3,71) = 0,29^2 + 2\cdot 3,71^2 + 2\cdot 0,29 \cdot 3,71 – 6 \cdot 0,29 -16 \cdot 3,71 = 9,66 \)
Und da wir sagen können, dass \( 9,66 < 12 \) haben wir definitiv eine Verbesserung gefunden.
Nun fängt das Verfahren von Vorne an, mit dem neuen, besseren Punkt als Startpunkt.
Und dieses Verfahren wiederholt man nun solange bis man meint das der Wert nun genau genug ist. Dafür definiert man eine Grenze bis zu welcher Genauigkeit man den Wert bestimmen möchte. Die Different der aufeinanderfolgenden, verbesserten Funktionswerte darf dann nicht größer sein als diese Grenze.
Wenn ein Wert mal keine Verbesserung bringt wird die Schrittweite, also unser \( \lambda \) halbiert.
Das Minimum für diese Funktion liegt übrigens im Punkt \( M = (-2, 5) \). Unten findet ihr den kompletten Rechenweg bis zu einer Genauigkeit von \( 4 \cdot 10^-3 \). So könnt ihr das Gradietenabstiegsverfahren üben und verinnerlichen.
EIn kleiner Tipp: Das Tool Wolfram Alpha hat ein Widget zum Bestimmen von lokalen Extrempunkten, so könnt Ihr also gut überprüfen ob Ihr auf das Richtige Ergebnis kommt.
Unter diesem Link kommt ihr direkt dorthin.
Für unsere Beispielfunktion liefert es die Folgende Lösung:

Solltet ihr die Darstellung der Funktion noch nicht kennen sei dir gesagt das es sich dabei um die Darstellung einer Funktion durch ihre Höhenlinien handelt. Das heißt die Farben symbolisieren (wie bei einer Höhenkarte im Atlas) die unterschiedlichen Höhenlagen einer mehrdimensionalen Funktion.
Lösung
So, ich hoffe ich konnte dir das Gradientenabstiegsverfahren damit etwas näher bringen. Sollten noch Fragen offen sein, oder du hast irgendwelche Anmerkungen zu dem Beitrag, hinterlass doch einfach ein Kommentar. Ich würde mich freuen.
Vergiss nicht den Newsletter zu abonnieren wenn du immer auf dem neusten Stand bleiben willst.
Sonst sehen wir uns beim nächsten mal.

Hi, ich glaube bei deinem aufgestelltem Gradienten in Teil 1. hast du die 2 vor dem x für die Ableitung nach x im „Gesamtgradienten“ vergessen. Hoffe der Satz war einigermaßen lesbar und ich liege nicht daneben. Vielen Dank aber! Die Erklärung ist super!
Danke für den Hinweis, ist schon geändert. Freut mich wenn dir der Beitrag gefällt. Immer her damit sollte es noch eher Themen geben die dich interessieren:D